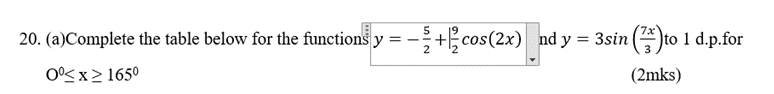GET THE KCSE PREDICTION MATHEMATICS Paper 2 MARKING SCHEMES HERE
Bunyore
SECTION 1 (50marks)
(Answer all questions in this section)
- The length and width of a rectangle were measured as 12.4cm and 5.0cm respectively. Find to 4 significant figures, the percentage error in calculating the area of the rectangle (3mks)
- The co-ordinates of a point A is (2, 8, 3) and B is (-4, -8, -5). A point P divides AB externally in the ratio 7: 3. Determine the co-ordinates of P (3mks)
- Solve for x:
Solve for x: (log3x)2 – ½ log3 x= 3/2 (3mks)
- A circle is tangent to the y – axis and intersects the x- axis at (2,0) and (8,0). Obtain the equation of the circle in the form x 2 + y 2 +ax +by +c = 0, where a, b and c are integers (4mks)
- Solve for X in the equation:
2 Sin2x – 1 = Cos2x + Sin x, for 0 ≤ x ≤ 360 (3mks)
- Make P the subject of the formula
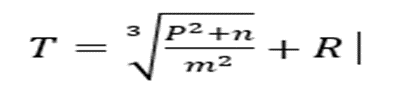
- (3mks)
- The figure below represents a flower garden ABC. A tap T is to be placed inside the triangle such that it is nearer A than B and angle ATB is greater than 120. By construction, show the region T where the tap can be positioned. (4mks)
- PQRS is a rectangle whose area 170cm2. The internal rectangle measures (x+5)cm by (x-2)cm
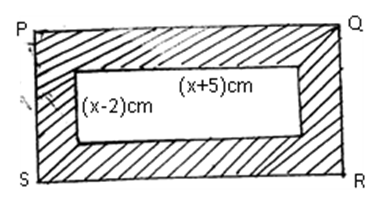
Determine the area of the shaded part if the thickness of this part is 0.1x cm (4mks)
- Find the length of an arc of a circle which subtends an angle of 0⋅8 radians at the center of the circle. The radius of the circle is 15 cm. (2mks)
- A map has a scale of 1: 25 000. On this map a square piece of land is represented by an area of 2cm2. Calculate the actual area in hectares of the land. (2mks)
- A dealer has two types of grades of tea, A and B. Grade A costs shs.140 per kg while grade B costs shs.160 per kg. Determine the ratio he should mix A and B so that he makes a 60% profit when he sells the mixture at shs.232 per kg. (3mks)
- The data below shows marks scored by 8 form four students in Molo district mathematics contest44, 32, 67, 52, 28, 39, 46, 64. Calculate the mean absolute deviation of the data. (3mks)
- A variable y varies as the square of x and inversely as the square root of z. Find the percentage change in y when x is changed in the ratio 5:4 and z reduced by 19% (3mks)
- Simplify
- leaving your answer in the form where a, b and c are rational numbers.
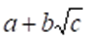

- (3mks)
- When a man is standing at a point x, he observes that the angle of elevation of the top of a flag post is 13o, he walks 120 m towards the flag post and the angle of elevation is 30o. If the eyes of the man are 1.5m from the ground, find the height of the flag post. (4mks)
- Findthe value of x given that T is a singular matrix. (3mks)
- When a man is standing at a point x, he observes that the angle of elevation of the top of a flag post is 13o, he walks 120 m towards the flag post and the angle of elevation is 30o. If the eyes of the man are 1.5m from the ground, find the height of the flag post. (4mks)
- Findthe value of x given that T is a singular matrix. (3mks)
T =
SECTION II 50 marks – Mathematics Paper 2 KCSE Prediction
(Answer only five questions in this Section)
- A tank has two water taps P and Q and another tap R. When empty the tank can be filled by tap P alone in 5 hours or by tap Q in 3 hours. When full the tank can be emptied in 8 hours by tap R.
- The tank is initially empty. Find how long it would take to fill up the tank
i) If tap R is closed and taps P and Q are opened at the same time. (2mks)
ii) If all the three taps are opened at the same time.Giving your answer to the nearest minute. (2mks)
b) Assume the tank initially empty and the three taps are opened as follows;
P at 8:00 am, Q at 9:00 am and R at 9:00 am
- Find the fraction of the tank that would be filled by 10:00 am. (3mks)
ii) Find the time the tank would be fully filled up. Give your answer to the nearest minute.
In the figure below, G is the center of the circle. <DCB = 50˚, <AGB = 63˚ and <FEC = 111˚

(a)Determine the size of the following angles
- FAC (1mk)
- BAC (1mk)
- ACB (1mk)
- ACF (1mk)
- AFC (1mk)
(b)DC is a tangent to the circle at C and its length is 6cm. AD is a straight line and chord AB is 3.1cm. Determine
(i) The length of BD (2mks)
(ii) Area of triangle ABC (3mks)
- The table below shows the income tax rates in a certain year.
| Annual taxable income in Kenya shillings | Tax rate in % |
| 0-144000 | 0% |
| 144 001 -300 000 | 10 |
| 300 001 – 468 000 | 15 |
| 468 001 -648 000 | 20 |
| 648 001-840 000 | 25 |
| Above 840 000 | 30 |
During that year Kurenta’s annual gross tax in sixth band was Shs 108 000.
- Determine Kurenta’s annual gross tax. (3mks)
- If he enjoyed annual relief of Shs. 21 000, determine his monthly net tax (P.A.Y.E)(2mks)
- Kurenta had a basic salary of Shs X Shs p.a. and enjoyed non-taxable allowances that is equivalent to 45% of basic salary. Determine Kurenta’s gross salary p.m. (3mks)
(d)The following deductions were also made from Kurenta’s salary every month: Co-operative shares 8 000, Co-operative loans 12 000, Pension scheme 4 000, Union dues 2000. (2mks)
Determine Kurenta’s monthly net salary during that year.
- (a)Complete the table below for the functions
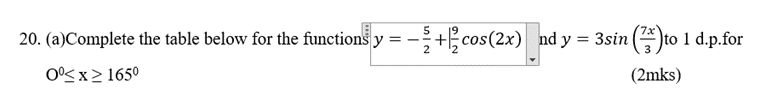
- (2mks)
| 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | ||
| 2 | 1.4 | -2.5 | -4.8 | -6.4 | -7 | -6.4 | -2.5 | 1.4 | ||||
| 1.7 | 2.8 | 2.9 | 1.9 | -2.7 | -2.9 | -2.1 | 1.3 |
DRAW THE GRAPH OF