SECTION I (50 MARKS)

Answer all the questions in this section

1. Use mathematical tables to evaluate;                                                      (3mks)

• A wholesaler sold a cell phone to a retailer making a profit of 20%.  The retailer later sold the cell phone for Ksh.3120 making a profit of 30% calculate the amount of money the wholesaler had paid for the cell phone.                                                                                                                   (3 mks)

• A piece of plot in Gilgil measuring 27m by 16m is to be divided into smaller rectangular units leaving no remainder. Calculate the highest number of smaller units whose dimensions are each greater than 1m that can be obtained from the plot.                                                      (3mks)

• A Kenyan bank buys and sells foreign currencies as shown below.

                                                Buying                                                Selling

      1US Dollar                                    76.38                                       75.19

      1UK pound                                   132.92                                                 132.95

      A tourist arrived in Kenya from Britain with 126,000 UK  sterling pounds. He converted the pounds into Kenyan shillings. While in Kenya he spent  of the money. He changed the balance to US dollars. Calculate to the nearest Dollar, the amount he received.                                     (3 mks)

• The figure below shows quadrilateral ABCD in which AB = 6cm. BC = , CD = DA and angle ADC = angle BCD = 90⁰.

1. The exterior angle of a regular polygon is (c – 50)° and the interior angle is (2c + 20)°.  Find the number of sides of the polygon.                                                                                                         (3 mks)

•  simplify:                                                                                                         (3 mks)

• The diagram below represents a right pyramid on a square base of side 3cm. The slant edge of the pyramid is 4cm.

• Draw a labelled net of the pyramid.                                                                           (2 Mks)

On the net drawn, measure the height of a triangular face from the top of the pyramid.                  

1. The mass of two similar solids are 324g and 768g.  Find

(a)        height of the smaller solid if the height of the bigger solid is 20cm.                         (2 mks)

            (b)        the surface area of the smaller solid if the surface area of the bigger solid is 40cm².                                                                                                                                                (2 mks)

• State all the integral values  which satisfy the inequality 3a + 2< 2a + 3 < 4a + 15(3mks)

                                                                                                4                  5 6

• The length of a rectangle is (3x+1)cm, its width is 3cm shorter than its length. Given that the area of the rectangle is 28cm², find its length.           `                                                                       (3marks)                                                               

• The curved surface area of a cylindrical container is 1980cm².if the radius of the container is 21cm, calculate to one decimal place the capacity of the container. (take )                       (4 marks)

•  Using a ruler and a pair of compasses only, draw a line AB = 7cm long. Construct  BAC = 67.5⁰. Use line AC to divide AB into 3 equal parts.                                                              (2 mks)

• Given that Sin (x + 4⁰) = Cos (3x) ⁰. Find tan (x + 40⁰) to 4 s.f.                                      (3 mks)

• Given that                 (3 mks)

• The position vector OA = – 3a i + b j, OB = 6a i + 4b j and OC = 15a i + 7b j, where a and b are scalars. Find in column form;

       (i) AB                           (1 mk)

 (ii) AC                                                 (1 mk)

Hence show that A,B and C are collinear.                                                                   (1 mk)

SECTION II (50 MARKS)

Answer any five questions in this section

1. A straight line passes through the points (8, -2) and (4, -4)
2. Write its equation in the form ax + by + c = 0 where a, b and c are integers.            (3 Mks)

• If the line in (a) above cuts the x-axis at point p, determine the coordinates of P.    (2 Mks)

• Another line which is perpendicular to the line in (a) above passes through point P and cuts the y-axis at the point Q. Determine the coordinates of point Q.                                               ( 3 Mks)

• Find the length of QP                                                                                                 (2 Mks)

• A group of people planned to contribute equally towards buying land at a price of Shs 180,000. However 3 members of the group withdrew from the project. As a result, each of the remaining members were to contribute KShs. 3000 more.
• Find the original number of members in the group.                                                   (6 Mks)

• How much would each person have contributed if the 3 people had not withdrawn.(2 Mks)

• Calculate the percentage increase in the contribution per person caused by the withdrawal.                                                                                                                                                     (2 Mks)

• a)   The figure below is a velocity time graph for a car.

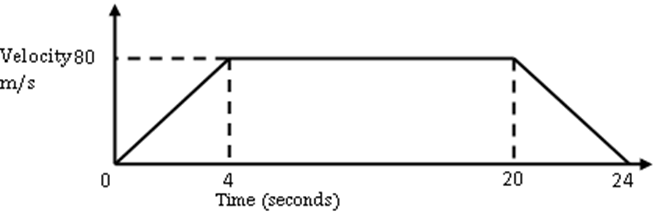
(i)   Find the total distance travelled by the car.                                                                      (2 Mks)

      (ii) Calculate the deceleration of the car.                                                                         (2 Mks)

      (b)  A car left Nairobi towards Eldoret at 7.12 a.m. at an average speed of 90km/h. At 8.22 a.m, a bus left Eldoret for Nairobi at an average speed of 72km/hr. The distance between the two towns is 348km. Calculate:

      (i) the time when the two vehicles met.                                                                          (4 Mks)

      (ii)  the distance from Nairobi to the meeting place.                                                        (2 Mks)

1. Triangle PQR has vertices at P (2,3), Q(1,2) and R(4,1), while triangle P^IQ^IR^I has vertices P^I(-2,3),Q^I(-1,2), R^I(-4,1)
2. (i)   Draw triangle PQR and P^IQ^IR^I on the grid provided.                                         (2 Mks)

            (ii)  Describe fully a single transformation which maps triangle PQR onto triangle P^IQ^IR^I.                                                                                                                                           (2 Mks)

• (i)   On the same grid, draw triangle P^IIQ^IIR^II the image of PQR under a reflection on the line y + x = 0                                                                                                                                    (2 Mks)

            (ii)  Describe fully a single transformation which maps triangle P^IIQ^IIR^II onto triangle P^IQ^IR^I.                                                                                                                                                 (2 Mks)

• On the same grid, draw triangle P^IIIQ^IIIR^III the image of P^IIQ^IIR^II under a reflection on the line x = 0                                                                                                                                    (2 Mks)

1. A trader bought 8 cows and 12 goats for a total of Ksh.294,000.  If he had bought 1 more cow and 3 more goats he would have spend Ksh.337,500.

      (a)  Form two equations to represent the above information.                                           (2 mks)

      (b)  Use matrix method to determine the cost of a cow and that of a goat.                      (4 mks)

(c) The trader sold the animals he had bought making a profit of 40% per low and 45% per goat.

      (i)   Calculate the total amount of money he received.                                                     (2 mks)

      (ii)  Determine his profit in Kenya shillings.                                                                     (2 mks)

• Three warships A,B and C are at the sea such that ship B is 500km on a bearing N30E from ship A.  Ship C is 700km from ship B on a bearing of 120^o.An enemy ship D is sighted 800km due south of ship B.

a)   Taking a scale of 1cm to represent 100km, locate the positions of ships A, B, C and D.(4 mks)

b)   Find the bearing of:

      i)    Ship A from D                                                                                                            (1 mk)

      ii)   Ship D from C                                                                                                            (1 mk)

c)   Use scale drawing to determine the distance between

      i)    D and A                                                                                                                       (1 mk)

      ii)   C and D.                                                                                                                      (1 mk)

d)   Measure angle DAC and angle BCD                                                                                (2 mks)

• The figure below shows a tumbler with diameters 6cm and 10cm and height 15cm.

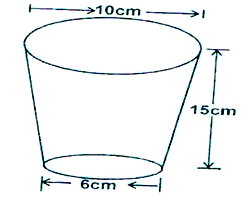
• If it is filled with water, what area is in contact with water?                                     (7 Mks)

• Find the volume of the tumbler.                                                                                 (3 Mks)

• The following are masses of 25 people taken in a clinic.

20              35        29        45        60

66              56        29        48        37

59              64        24        28        32

35              45        48        52        55

54              55        36        39        35

      (a)  Using a class width of 8 and starting with the lowest mass of the people. Make a frequency distribution table for the data.                                                                                               (3 Mks)

      (b)  Calculate the mean mass of the people.                                                                               (2 Mks)

      (c)  On the grid provided, draw a histogram and a frequency polygonto represent the information.                                                                                                                                     (5 Mks)