Get The Marking Schemes Here
1. Simplify (3marks)

2. Given that Cos(x -20)° = Sin(2x + 32)° and x is an acute angle, find Tan (x – 4)° (3marks)
3. Find a quadratic equation where roots are 1.5 + √2 and 1.5 – √2, expressing it in the form ax2 + bx + c = 0, where a, b and c are integers (3marks)
4. The length and breadth of a rectangular flower garden were measured and found to be 4.1m and 2.2m respectively. Find the percentage error in its area (3marks)
5. Determine the inequalities that define the unshaded region in the diagram below. (3mks)

6. Solve the following simultaneous equations (3mks)
x + y=3
6y −xy=70
7. Given that log 5=0.6990 and log7=0.8451, find log 24.5 (3mks)
8. Simplify completely. (3mks)
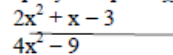
9. A 890kg culvert is made of a hollow cylindrical material with outer radius of 76cm and an inner radius of 62cm. It crosses a road of width 3m. Determine the density of the material used in its construction in Kg/m3 correct to one decimal place. (3marks)
10. In a mixed school there are 900 students; out of these 600 are girls.
(a) Find the ratio of boys to girls. (2marks)
(b) What is the percentage of boys in this school? (1mark)
11. Lines K whose equation is 2𝑦 − 6 = 4𝑥 is perpendicular to another line Q. Find the equation of line Q if it passes through point. (-2,7). (3 marks)
12. The marked price of a car in a dealers shop was Ksh.450 000. Kawira bought the car at 7% discount. The dealer still made a profit of 13%. Calculate the amount of money the dealer had paid for the car to the nearest shillings. (3marks)
13. Given that 8≤ 𝑦≤12 and 1≤𝑥≤6, find the maximum possible value of; (3marks)
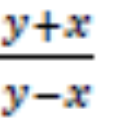
14. The length of a rectangle is (𝑥+1) cm. its width is 3cm shorter than its length. Given that the area of the rectangle is 22cm, find its length using completing the square method. (4marks)
15. A car uses 1 litre of petrol for every 8 kilometres. The car was to travel 480 kilometres and had 15 litre of petrol at the beginning of the journey. Each litre of petrol cost sh. 112.00. How much did it cost for the extra petrol added? (3mks)
16. The figure below is a velocity – time graph for a car. ( not drawn to scale).
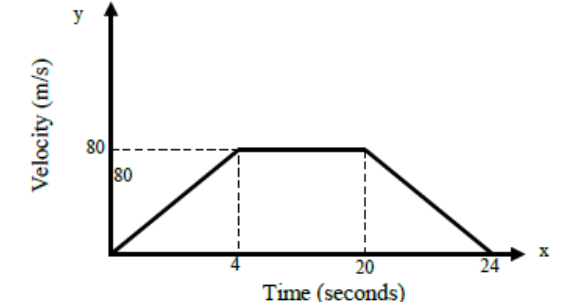
a).Find the total distance traveled by the car? (2 Marks)
(b) Calculate the deceleration of the car. (2 Marks)
SECTION II (50 MARKS)
Answer ANY FIVE questions in this section.
17) In a triangle ABC, BC=8cm, AC=12cm and angle ABC=120°
a) Calculate the length of AB, correct to one decimal place (4marks)
b) If BC is the base of the triangle, calculate correct to one decimal place
i. The perpendicular height of the triangle (2marks)
ii. The area of the triangle (2marks)
iii. The size of angle ACB (2marks)
18. The diagram below shows a frustum which represents a bucket with an open end diameter of 36cm and a bottom diameter of 24cm. The bucket is 30cm deep as shown and it is used to fill an empty cylindrical tank of diameter 1.4m and height 1.2m.
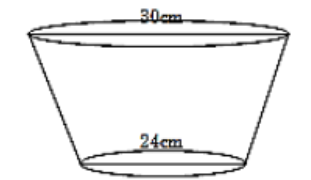
- leaving 𝜋 in your answer , calculate
- The capacity of the bucket in litres. (6mks)
(ii) The capacity of tank in litre. (2mks)
(b) Determine the number of buckets that must be drawn in order to fill the tank. (2mks)
19. The table below shows the age groups and number of people who are HIV/ AIDSpositive, in a certain sub county in Kenya.
a).State the modal age group. (1mark)
b) Calculate the mean age of the people who are HIV/AIDS Positive. (3marks)
c) Calculate the median of the age group. (3marks)
d) Draw on the grid provided a histogram to represent the above information. (3marks)
(The grid to be provided by the examiner)
20. The diagram below shows a solid made of a hemisphere and a cylinder. The radius of both the cylinder and the hemisphere is 3cm. The length of the cylinder is 12cm.

a).i) Calculate the volume of the solid. (3marks)
ii) The solid fits in a box in the shape of a cuboid 15 cm by 6cmby 6cm. Calculate the volume
of the box not occupied by the solid correct to four significant figures. (2marks)
b) i) Calculate the total surface area of the solid correct to four significant figures. (3marks)
ii) The surface of the solid is to be painted. One millilitre of paint covers an area of 8cm2 .The
cost of paint is Ksh 900 per litre. Calculate the cost of the paint required. (2marks)]
21. Members of a group decides to raise k£ 100 towards a charity. Five of them were unable to contribute. Each of the rest had therefore to pay k£ 1 more, in order to raise the same amount.
a) If the original number of member was x, writes downs:
i) An expression of how much each was originally to contribute. (1mark)
ii) Two distinct expressions of how much each contributed after the five pulled out.(2marks)
b) Calculate the value of x. (3marks)
c) Solve the equation (4marks)
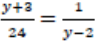
22. Arc of a circle of radius 40cm subtends an angle of 126° at the centre of the circle. Using 𝜋= ;
(a) Calculate:
(i) The length of the arc. (2 marks)
ii).The area of the sector. (2 marks)
(b) The sector is folded to form a cone.
Calculate:
i).The radius of the base of the cone. (2 marks)
ii).The height of the cone. Correct to 2 decimal places (2 marks)
iii).The capacity of the cone in litres correct to 2 decimal places. (2 marks)
23. The figure below shows a triangle ABC inscribed in a circle. AC = 10cm, BC = 7cm and AB = 10cm.

a).Find the size of angle BAC. (3mks)
b).Find the radius of the circle. (2mks)
c).Hence calculate the area of the shaded region. (5mks)
24. A tailor bought a number of suits at a cost of sh.57, 600 from ken-suit wholesalers. Had he bought the same number of suits from Umoja wholesaler it would costed him sh.480 less per suit. This would have enabled him to buy 4 extra suits for the same amount of money.
(a) Find the number of suits the tailor bought. (6 mks)
(b) The tailor later sold each suit for shs. 720 more than he had paid for it. Determine the percentage profit he made. (4 mks)