Get Marking Schemes From Here
Attempt all the questions in the spaces provided.
1. Solve for x in the equation: (3 mks)
32(x-3) X 8(x+4) = 64 ÷ 2x
2. Simplify without using a calculator or a mathematical table
Sin 90o Cos 45o
Sin 45o (2 mks)
3. A line which joins the point A(3, k) and B(-2, 5) is parallel to another line whose equation is
5y + 2x = 10. Find the value of K. (3 mks)
4. A group of 5 people can do a piece of work in 6 hours. Calculate the time a group of 8 people,
working at half the rate of the first group could take to complete the same work. (3 mks)
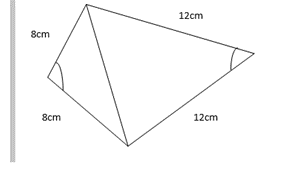
5. Calculate the area of the shape below. (3 mks)
6. The length of a minute hand of a clock is 3.5cm. Find the angle it turns through if it sweeps an
area of 48cm. (Take π = 22/7) (2 mks)
7. Two years ago, Jane was twice as old as John. If the sum of their ages 5 years from now will be
44 years, calculate their present ages. (3 mks)
. . .
8. Express 1.93 + 0.25 as a single fraction. (3 mks)
9. The surface area of two similar bottles are 12cm2 and 108cm2 respectively. If the larger one has a volume of 810cm3, find the volume of the smaller one. (3 mks)
10. Simplify the following expression
7x – 7xy
7 – 7y (2 mks)
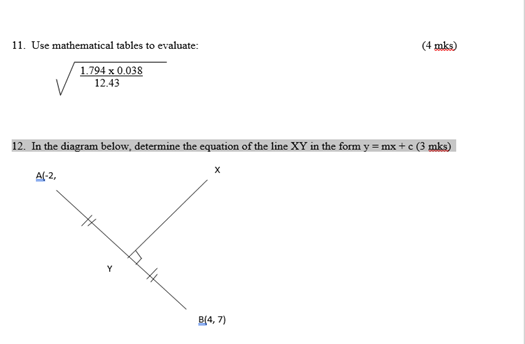
11. Use mathematical tables to evaluate: (4 mks)
13. An aircraft flying onto an airport calls out the control tower and says it is at height of 500m
above the tower. If its horizontal distance from the tower is 8km, calculate the angle of
elevation from the tops of the tower. (3 mks)
14. The figure below shows an isosceles triangle in which AB = AC = 6cm. Angle BAC = 80˚.
Calculate the length of BC.
SECTION II(30 MARKS)
Choose any three questions only.
16. The vertices of a triangle PQR are P(0, 0) Q(6,0) and R(2,4)
(a) Draw triangle PQR on the grid provided. (1 mk)
(b) Triangle P’Q’R’ is the image of a triangle PQR under an enlargement scale factor ½ and
centre (2,2) write down the coordinates of P’Q’R’ and plot on the same grid. (3 mks)
(c) Draw triangle P”Q”R” the image of triangle P’Q’R’ under a positive quarter turn about
point (1,1) (3 mks)
(d) Draw triangle PIIIQIIIRIII the image of P”Q”R” under a reflection in the line y = 1.
17. In a school, there are 1250 students, each student contributed sh 380 towards a welfare
programme. The money contributed was used to purchase 75 bales of maize flour which was
shared equally among 50 families. One bale of maize flour contains 12 packets and costs sh
1050. The remaining amount was shared equally among 125 students as bursary. Calculate:
(a) The total amount collected. (2 mks)
(b) The total number of maize flour bought (2 mks)
(c) The number of packets each family got. (2 mks)
(d) The amount of money that remained. (2 mks)
(e) The amount of bursary that each student got. (2 mks)
18. Find the area in hectares of a maize field whose measurements are shown in the field book
below. The baseline PQ is 300m long. (10 mks)
| Q | ||
| 250 | 70B | |
| C100 | 180 | |
| 80 | 150A | |
| P |
19. The marked price of a sewing machine is sh 30,000. A discount of 10% is given on cash
payment. The sewing machine can also be bought on hire purchase. The hire purchase terms
requires a deposit of sh 10500 followed by 12 equal monthly installments of sh 2150 each.
(a) Calculate:
(i) The cash price of the sewing machine. (2 mks)
(ii) The hire purchase value of the sewing machine. (3 mks)
(b) Korir bought the sewing machine by cash while Akinyi bought it on hire purchase. How
much did Akinyi pay for the machine than Korir? (3 mks)
(c) Calculate the percentage increase in hire purchase price over the marked price.(2 mks)
20. (a) Complete the following tables for the equations:
(i) y = 5x – 7
(ii) y = 9 – 3x
Table 1
| X | -2 | -1 | 0 | 1 |
| y | -12 | 7 | ||
| (x,y) | (-1, -12) | (0, -7) |
Table 2
| X | -2 | -1 | 0 | 1 |
| y | 13 | 7 | ||
| (x,y) | (-2, 13) | (1, 7) |
(b) On the same grid, draw the graphs of: (4 mks)
(i) y = 5x – 7
(ii) y = 9 – 3x
(c) Use your graphs to solve the following simultaneous equations. (2 mks)
5x – y = 7
3x + y = 9