BOYLE’S LAW.

1. State Boyle’s Law

The pressure of a fixed mass of a gas is inversely proportional to its volume at a constant temperature.

2. State how the pressure of a fixed mass of gas can be increased at constant temperature.                                                           (1mk)

3. An air bubble expands as it rises to the surface of water in a deep pond. State the cause of this given that the temperature remains constant.  (1mk)

Decrease in pressure due to water as the bubbles rises to the top it expand since pressure increases with depth.

4. When an inflated balloon is placed in a refrigerator, it is noted that its volume reduces. Use kinetic theory to explain this observation.                    (1mk)

5. Show that the density of a fixed mass of gas is directly proportional to the pressure at constant temperature.

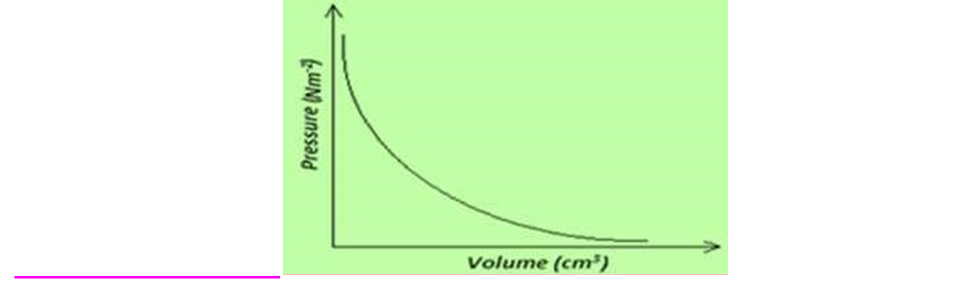
6. Draw axes and sketch the P – V graph for a gas obeying Boyle’s Law.

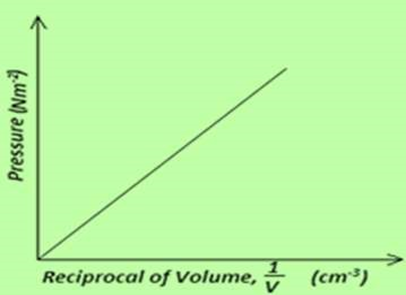
7. Draw axes and sketch a graph of pressure (P) against reciprocal of volume (1/v) for a fixed mass of an ideal gas at a constant temperature.

8. On the axes provided, sketch a graph of PV against V for ideal gas in which

                       Boyle’s law is obeyed.                                         (1mk)

                                           V

9. On the axis below, sketch a graph to show how the pressure of a fixed mass of a gas varies with volume at constant temperature.              (1mk)

                                           V

10. A diver at the bottom of a swimming pool releases an air bubble of volume 2cm³.  As the air bubble rises, its volume increases to 5cm³ at the surface of the pool.  Explain this observation.

11. A bubble at the bottom of a pond rises to the surface of the pond. If the volume, as it just reaches the surface is double that at the bottom of the pond; estimate

the depth of the pond. (Assume uniform pond temperature Atmospheric

                      pressure 100kPa)                                                              (5mk)

12.   A bubble of air of volume 1cm³ is released by a deep-sea diver at a depth where the pressure is 30 atmospheres. Assuming its temperature remains constant  (T₁ = T₂) what is its volume just before it reaches the surface where the pressure

                   is 1.5 atmosphere?                               (3mks)

13. A hand pump suitable for inflating a football has a cylinder which is 0.24m in length and an internal cross-sectional area of 5.0 x 10^-4 m². To inflate the football the pump handle is pushed in and air is pumped through a one-way valve.  The valve opens to let air in to the ball when the air pressure in the pump has reached 150 000Pa. (Assume the air temperature remains constant}

a) If the pressure in the pump is initially 100 000 Pa, calculate how far the piston must be pushed inwards before the one way valves opens.

Let the initial length of hand pump be Y

V₁=0.24 x 5.0 x 10^-4 m³

P₁=100,000 Pa

P₂=150,000Pa

V₂= (Y x 5.0 x 10^-4) m³

By boyle’s law: P₁V₁=P₂V₂

100,000 x (0.24 x 5×10^-4)=150,000 × (Y x 5.0 x 10^-4)

Y= 0.16

Length piston moved inwards=0.24-0.16=0.08 m

 (b) When the one-way valve opens the total pressure in the cylinder will be 150 000 Pa. What force will be exerted on the piston by the air in the cylinder?

GAS LAWS ‘BOYLE’S LAW.‘

14. Air is trapped inside a glass tube by a thread of mercury 240mm long. When the tube is held horizontally, the length of the air column is 200mm.

Given that the atmospheric pressure is 760mmHg and the temperature is kept constant, calculate the length of air column when the tube is held;

                  (i) Vertical with the open end up                                             (3mk)

Atmospheric pressure =760 mmHg

 240 mm

 L    P₂=(760+240)=1000mmHg

15. The pressure of helium gas of volume 10cm³ decreases to one third of its original value at a constant temperature.  Determine the final volume of the gas.

Solution 

V₁=10 cm³

Let initial pressure=P

New value of pressure= 1/3P

By boyle’s law: P₁V₁=P₂V₂

10×P=1/3P× V₂ V₂=30 cm³

16. A balloon seller has a cylinder of helium gas which he uses to blow up his balloons. The volume of the cylinder is 0.10m³. It contains helium gas at a pressure of 1.0 x 10⁷Nm^-2. The balloon seller fills each balloon to a volume of 1.0 x 10^-2m³ and a pressure of 2.0 x 10⁵N/m²

• Explain in terms of particles how the helium in the cylinder produces a pressure                                                                        (1mk)

ü Pressure is produced when particles collide with each other and with the wall of the cylinder.

b. Calculate the total volume that the helium gases occupy at a pressure of 1.2 x 10⁵ N/m². Assume the temperature of  the helium does not change.

                        

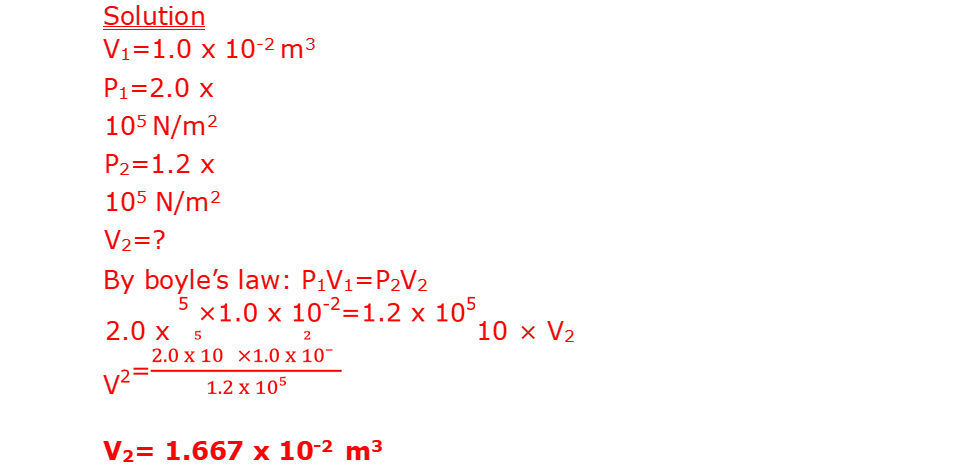
(c)    Calculate the number of balloons of volume 1.0 x 10^-2m³ that the balloon seller can fill using the gas                                                   (2mk)

          

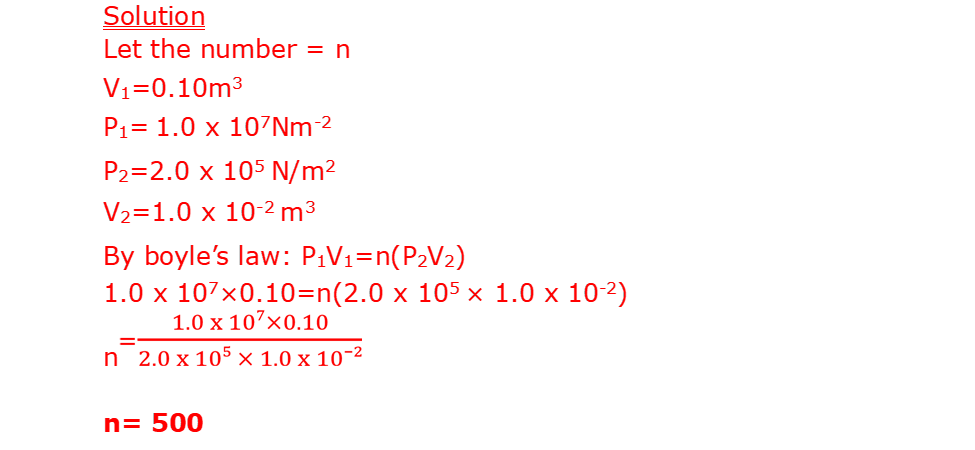
17. An air bubble is released at the bottom of a tall jar containing a liquid. The height of the liquid column is 80cm. The volume of the bubble increase from

0.5cm³ at the bottom of the liquid to 1.15cm³ at the top. The figure below shows the variation of pressure P, on the bubble with the reciprocal of volume 1/V as it rises in the liquid.

              

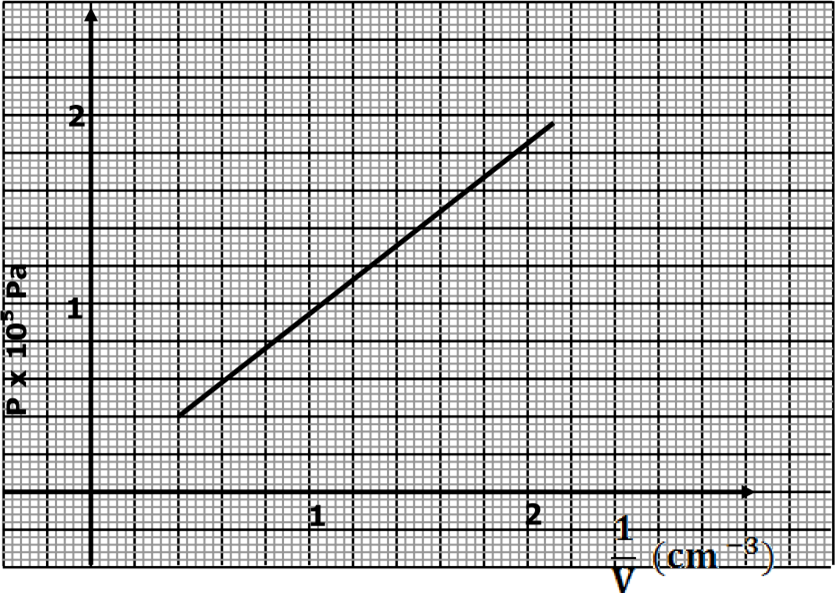
(a)   State the reason why the volume increases as the bubble rises in the liquid column.                                             (1mk)

ü Decrease in pressure exerted  on the bubbles by the liquid column as it rises to the top.

(b)         From the graph, determine the pressure on the bubble.

• At the bottom of the liquid column;   (2mk)
  • (1.8+0.16) ×10⁵  =1.96×10⁵ Pa
• At the top of the liquid column.                                              (1mk) ü 0.4×10⁵     =4.0×10⁴ Pa
• Hence determine the density of the liquid in kgm^-3(3mk)
  • Height = 80 cm, g=10,  
  • Pressure of the air bubble at the bottom=1.96×10⁵ Pa
  • Pressure =ρhg
  • 1.96×10⁵=ρ×0.8×10

ü ρ=2.45×10³ kg/m³

 (iv)  What is the value of the atmospheric pressure of the surrounding?  (1mk) ü (1.96×10⁵ Pa-4.0×10⁴ Pa)=1.56×10⁵ Pa

       18. Set up in figure is used to verify Boyle’s law  

                                                   

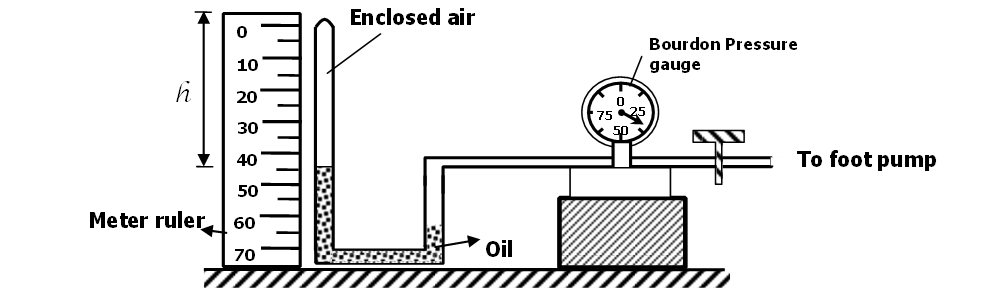
The pressure, P of a fixed mass of a gas at a constant temperature T = 300K is varied continuously. The corresponding values of P and the volume (V) of the gas are shown in the table below.

Pressure, P (x105N/m2)	2.0	2.5	3.0	3.5	4.0	4.5
Volume, V(M3)	0.025	0.02	0.017	0.014	0.012	0.011
I -3 /V (M )	40	50	58.8	71.4	83.3	90.9

• Complete the table above by filling in the values of  ^I/_V (1mk)

• Plot a graph of pressure (y – axis) against ^I/_V             (5mk)

          

Determine the gradient of the graph                           (3mks)        Slope =

 (iv) Given that the equation of the graph is PV = 2RT where R is a constant, use your graph to determine the value of R.                                (3mks)

From the graph, it is a straight line, Y=mx+c

                                                                    2RT= Slope/Gradient 

                                            2×300K×R=5.3191 × 10³ N/m

                                                           600K×R=5.3191 × 10³ N                                                     R=8.8652Nm^-1k^-1 or J/K

• State the unit of R.                      (1mk)

ü Nm^-1k^-1 or J/K

• Estimate the pressure of the air column when the length of the air is zero (2mk)

Pressure  =0 Pa

• From the graph, calculate the volume when the pressure 

                                   380,000N/m²                                                                                 (2mks)

3.8 x 10⁵ N/m²=70.1 m^-3 =0.01426m³

• State the two physical quantities which were kept constant (2mks) ü Mass and temperature